Assalamualaikum wr.wb saya aliya rahmah XI IPS 2 akan memberikan contoh soal penyelesaian kesamaan matriks, soal determinan matriks berordo 3x3 dan 2x2, soal kofaktor matriks beordo 3x3 dan 2x2, invers matriks berordo 3x3 dan 2x2.
-KESAMAAN MATRIKS-
1. Tentukanlah nilai x dan z yang memenuhi persamaan matriks berikut ini :
Pembahasan :
-1 + 6 = 2 + 2x
5 = 2 + 2x
3 = 2x
x = 3/2
3 + 2 = 3 + z + 1
5 = 4 + z
z = 1
2. Diketahui persamaan matriks sebagai berikut :
Tentukanlah nilai a, b, c, dan d.
Pembahasan :
-a + 3 = 10 ---> a = -7
c - 2 + 10 = -6
c = - 6 - 8
c = -14
b + 4 + b + c = -6
2b + c = -10
2b - 14 = -10
2b = 4
b = 2
2d + d = b - 2
3d = 2 - 2
d = 0
3. Tentukan nilai x yang memenuhi persamaan matriks di bawah ini.
Pembahasan :
Dari hubungan di atas, diperoleh
log (2a - 2) = 1
log (2a - 2) = log 10
2a - 2 = 10
a = 12/2 = 6
log (b-4) = log a
log (b-4) = log 6
b-4 = 6
b = 10
xlog a = log b
xlog 6 = log 10
xlog 6 = 1
x = 6
Jadi nilai x yang memenuhi persamaan di atas adalah 6
4. Berdasarkan persamaan matriks di bawah ini, tentukanlah nilai a, b, c, dan d.
Pembahasan :
2d + d = -2 + (-4)
3d = -6
d = -2
a + 2d + 3 = 10 + 2
a + 2(-2) = 12 - 3
a - 4 = 9
a = 9 + 4
a = 13
b + b + 3c = 16 + 8
2b + 3c = 24
c - 2 + 2 + b = -6 + 6
c + b = 0 ---> c = -b ---> substitusi ke persamaan 2b + 3c = 24
2b + 3(-b) = 24
2b - 3b = 24
-b = 24
b = -24 maka c = 24
Maka = 13. b = -24, c = 24, dan d = -2
5. Tentukan nilai a
Pembahasan :
a + 3ab + a2 = a - 2
a - a + 3ab + a2 + 2 = 0
a2 + 3ab + 2 = 0 ---> persamaan kuadrat
Agar persamaan di atas sanggup diselesaikan, kita cari nilai b terlebih lampau.
b + 4 + b = 6
2b = 6 - 4
b = 2/2 = 1
Persamaan kuadrat di atas menjadi :
a2 + 3a + 2 = 0
(a + 2) (a + 1) = 0
a = -2 atau a = -1
-DETERMINAN MATRIKS BERORDO 3X3 DAN 2X2-
6. Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

pembahasan:

7. Hitunglah berapa nilai determinan dari matriks ordo 2 x 2 berikut ini :

pembahasan:

8. Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

pembahasan:

det( A ) = ( 2 . 4 . 1 ) + ( 3 . 3 . 7 ) + ( 4 . 5 . 0 ) – ( 4 . 4 . 7 ) – ( 2 . 3 . 0 ) – ( 3 . 5 . 1 )
= ( 8 ) + ( 63 ) + ( 0 ) – ( 112 ) – ( 0 ) – 15
= – 56
jadi nilai determinan matriks berordo 3x3 diatas ialah -56
9. Hitunglah berapa nilai determinan dari matriks ordo 3 x 3 berikut ini :

pembahasan:

det( A ) = ( 1 . 1 . 2 ) + ( 2 . 4 . 3 ) + ( 3 . 2 . 1 ) – ( 3 . 1 . 3 ) – ( 1 . 4 . 1 ) – ( 2 . 2 . 2 )
= ( 2 ) + ( 24 ) + ( 6 ) – ( 9 ) – ( 4 ) – ( 8 )
= 11
Jadi, nilai determinan dari matriks ordo 3 x 3 di atas ialah = 11.
-KOFAKTOR MATRIKS BERORDO 2X2 DAN 3X3 -
10. Tentukan kofaktor dari minor matriks berikut ini :
pembahasan:
KEab = (-1)a+b x NEab
KE11 = (-1)1+1 x NE11 = (-1)2 x (-3) = 1 x -3 = -3
KE12 = (-1)1+2 x NE12 = (-1)3 x (-6) = -1 x (-6) = 6
KE13 = (-1)1+3 x NE12 = (-1)4 x (-3) = 1 x (-3) = -3
KE21 = (-1)2+1 x NE21 = (-1)3 x (-6) = -1 x (-6) = 6
KE22 = (-1)2+2 x NE22 = (-1)4 x (-12) = 1 x (-12) = -12
KE23 = (-1)2+3 x NE23 = (-1)5 x (-6) = -1 x (-6) = 6
KE31 = (-1)3+1 x NE31 = (-1)4 x (-3) = 1 x (-3) = -3
KE32 = (-1)3+2 x NE32 = (-1)5 x (-6) = -1 x (-6) = 6
KE33 = (-1)3+3 x NE33 = (-1)6 x (-3) = 1 x (-3) = -3
Maka kofaktornya adalah :
-INVERS MATRIKS BERORDO 3X3 DAN 2X2-
11. Menentukan matriks invers dari:
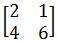
Jawaban :
Untuk menghitung kebalikan dari matriks, metode cepat digunakan. Sebelum menggunakan rumus matriks terbalik di atas. Pertama-tama kita harus menemukan nilai adjoin dahulu.
Untuk menemukan matriks invers 2×2 yang berdekatan, kita hanya perlu menukar atau memindahkan elemen yang posisinya ada di baris pertama kolom pertama dengan elemen-elemen di baris kedua kolom kedua.
Berikutnya, baris kedua dari kolom pertama dan baris pertama dari kolom kedua dikalikan dengan -1. Hasilnya adalah sebagai berikut.
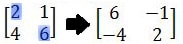
Selanjutnya, cari determinan matriks
det = (2 × 6) – (4 × 1)
= 12 – 4
= 8
Setelah nilai adjoin dan determinan matriks diketahui. Kemudian masukkan rumus matriks di atas. Hasilnya adalah :
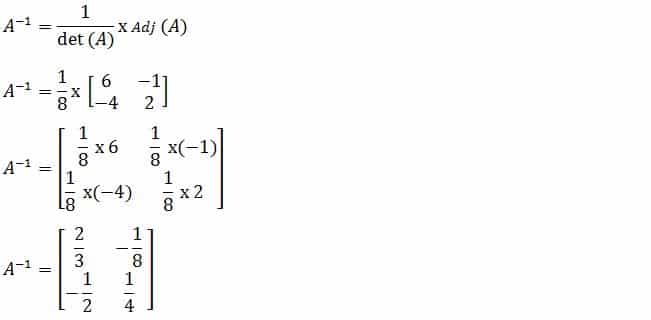
12. Matriks A dikenal sebagai berikut :
 Jawaban :
Jawaban :










Tidak ada komentar:
Posting Komentar