ASSALAMUALAIKUM WR.WB SAYA ALIYA RAHMAH XI IPS 2 SAYA AKAN MEMBERIKAN MATERI DAN SOAL SOAL METODE PEMBUKTIAN DALAM MATEMATIKA, SEMOGA BERMANFAAT.
Metode pembuktian
1 1.
Metode pembuktian langsung
2 2.
Metode pembuktian tidak langsung, terdiri dari:
a.
Dengan kontradiksi
b.
Dengan kontraposisi
3 3.Induksi matematika
LANGKAH-LANGKAH MELAKUKAN PEMBUKTIAN langsung
1 1.
Tulislah teorema yang akan dibuktikan
Contoh: jumlahh 2 bilangan genap adalah genap
2 2.
Tulislah dengan kata “bukti” sebagai pemisah antara
pembukti dan teorema yang ingin dibuktikan.
3 3.
Buktikanlah secara lengkap menyeluruh agar dapat
dimengerti beberapa keterangan pelengkap seperti:
- buat variabel dan
tipenya
Contoh: sembarang 2 bilangan, misalnya (m+n), variabel: (m+n)
- apabila ditengah tengan pembuktian ada suatu
sifat variabel, tulislah
Contoh: 2 sembarang bilangan (m+n) harus genap, maka m= 2r dan n = 2s
- apabila menggunakan sifat tertentu dalam suatu
persamaan maka tulis disebelah kanan
Contoh: m= 2r & n = 2s
(m+n) = 2r + 2s
= 2(r + s) → sifat distributif
- jika bertemu dengan ekspresi maka buat
variabel baru
Contoh: ekspresi penyingkiran= (r+s)
Misal : k= (r+s)
Sehingga (m +n) = 2(r+s)
=2k →
(m+n)=2k
- penyelesaian
Bukti: k=r+s
(m+n)=2r+s
(m+n)=2(r+s)
(m+n)=2(k)
Terbukti bahwa jumlah dar bilangan genap adalah bilangan genap juga
Metode pembuktian tidak langsung
1.
Dengan kontradiksi (bertentangan)
Langkah-langkah:
-
Misalkan negasi (-) dari statement yg
akan dibuktikan benar
-
Dengan langkah yg benar tunjukan hasil
pembuktian menimbulkan kontradiksi
-
Simpulkan bahwa statement yg dibuktikan
benar
Contoh: buktikan bahwa hasil kali 2
bilangan ganjil adalah ganjil
Bukti:
2 bilangan ganjil misal variabel m dan n
Andaikan hasil kalinya (m.n) adalah genap
M=2.k +1 dan n=2.S+1 K dan S adalah bilangan bulat
m.n = (2.k + 1)(2s+1)
=4.k.s
+ 2.S + 2K+1
=2(2.K.S+S+K)+1
= 2.P +1
Terbukti berapapun
bilangan bulat p, hasil kali 2 bilangan ganjil adalah ganjil. Hal ini
berkontradiksi dengan pengandaian tadi. Berarti pengandaiannya salah.
2.
Dengan kontraposisi
p⇾Q= 〜P⇾ -Q
untuk membuktikan
kebenaran P⇾Q Cukup tunjukan bahwa 〜p akan mengakibatkan -Q
Contoh: buktikan jika n kuadrat adalah bilangan ganjil
maka n adalah bilangan ganjil.
Bukti:
p= n kuadrat adalah bilangan ganjil
Q=n adalah bilangan
ganjil
p⇾Q
-Q= bilangan genap yaitu
n=2k
Sehingga:n kuadrat = (2k) kuadrat
n kuadrat =4k kuadrat
n kuadrat =2(2k)kuadrat
n kuadrat = 2(m)
n=2k kuadrat
pernyataan
〜p → -Q terbukti apabila p〜Q = 〜p ⇾ -Q maka terbukti pula p⇾Q
dimana hasil dari
kuadrat bilangan ganjil adalah bilangan ganjil
induksi matematika
Langkah-langkah:
1. Buktikan
n=1 benar
2. Misalkan
n=k pernyataan benar
contoh soal dan pembahasan
soal 1
Jika diketahui n adalah ganjil, maka n2 adalah .....
A. Ganjil
B. Genap
C. konstanta
D. A dan B benar
E. Tidak ada jawaban yang benar
Jawaban : A. Ganjil
n = 2k + 1. Akan ditunjukkan bahwa n2 ganjil.
n2 = (2k + 1)2
= 4k2 + 4k + 1
= 2(2k2 + 2k) +1.
Perhatikan bahwa n2 = 2(2k2 + 2k) +1.Karena k adalah bilangan bulat, maka (2k2 + 2k) juga pasti bilangan bulat, sehingga n2 adalah ganjil.
Soal 2
2..Pernyataan berikut yang sesuai dengan metode pembuktian kontradiksi adalah…
A. Jika p benar maka q benar
B. Jika ~q benar maka ~p juga harus benar
C. Membuat permisalan jika p maka q adalah benar
D. Suatu pembuktian untuk pernyataan yang memuat bilangan asli
E. Tidak ada jawaban yang benar
Jawaban A. Membuat Permisalan jika p maka q adalah benar
pembahasan: Kontradiksi
ialah dua hal dimana kedua hal tersebut tidak boleh sama sama benar
dalam waktu yang sama. Jadi, kita buat pemisalan jika p salah , q benar.
Jika kita buat ke dalam operasi logika p maka q (p → q) maka hasil yang didapat adalah benar.
Soal 3
Yang manakah yang termasuk dalam metode pembuktian tidak langsung…
A. Metode kontraposisi
B. Metode Disjungsi
C. Metode Equivalen
D. Metode Ingkarang
E. Metode Eliminasi
Jawaban : A. Metode kontraposisi
pembahasan:Karena metode kontraposisi termasuk metode pembuktian tidak langsung.
Soal 4
Bertikut ini adalah pernyataan yang benar mengenai prinsip induksi sederhana, kecuali.....
A. N ≥ 1 untuk bilangan bulat positif
B. P(1) bernilai benar
C. P(n+1) harus bernilai benar
D. N ≥ 1 untuk bilangan ganjil
E. P(n) harus bernilai benar
Jawaban : D. N ≥ 1 untuk bilangan ganjil
pembahasan:Karena,
salah satu ciri dari induksi sederhana adalah N ≥ 1 untuk bilangan
bulat positif, sementara pada pilihan D hanya untuk bilangann ganjil.
Soal 5
Apakah N3 +
2n adalah kelipatan 3 berlaku untuk n = 1 dan berlaku kelipatan 3 untuk
setiap bilangan bulat postitif n (menggunakan induksi matematika)…?
A. ya dan ya
B. ya dan tidak
C. tidak dan bisa jadi
D. tidak dan tidak
E. tidak ada jawaban yang benar
Jawaban : A. Ya dan ya
pembahasan: q Basis untuk n = 1 akan diperoleh :
13 + 2(1) = 3 yang merupakan kelipatan 3 (ya, berlaku n = 1)
q induksi (misalkan) untuk n = k asumsikan menjadi k3 + 2k = 3x
q adib untuk n = k + 1 berlaku :
(k + 1)3 + 2(k + 1) adalah kelipatan 3
(k3 + 3k2 + 3k+1) + 2k + 2
(k3 + 2k) + (3k2 + 3k + 3)
(k3 + 2k) + 3 (k2 + k + 1)
induksi
3x + 3 (k2 + k + 1)
3 (x + k2 + k + 1)
Kesimpulan : N3 + 2n adalah kelipatan 3 untuk setiap bilangan bulat positif n (ya, berlaku kelipatan 3).
Soal 6
Terdapat implikasi : Jika 15 habis dibagi 3, maka 15 adalah bilangan ganjil. kemudian 15 habis dibagi 3. Kesimpulannya adalah...
A. 15 habis dibagi 3
B. 15 adalah bilangan ganjil
C. 3 adalah bilangan ganjil
D. 3 habis dibagi 3
E. tidak ada jawaban yang benar
Jawaban : B. 15 adalah bilangan ganjil
pembahasan: Jika 15 habis dibagi 3, maka 15 adalah bilangan ganjil (p → q)
15 habis dibagi 3 (p )
∴ 15 adalah bilangan ganjil ( q)
Soal 7
misalkan p(n) benar untuk semua bilangan positif n ≥ 1 untuk bilangan 2 + 4 + 6 + ... + 2n = n(n + 1). p(n + 1) bernilai...
A. Benar
B. Salah
C. A dan B benar
D. A dan B salah
E. tidak ada jawaban yang benar
Jawaban : A. Benar
pembahasan: jika p(n + 1) benar, maka :
n = n + 1
2 + 4 + 6 + ... + 2n = n(n + 1)
2 + 4 + 6 + ... + 2n + 2(n + 1) = n + 1(n + 1 + 1)
2n + 2n + 2 = (n + 1) (n + 2)
2n + 2n + 2 = n (n + 1) + 2n + 2
= n2 + n + 2n + 2
= n2 + 3n + 2
= (n + 1) (n + 2) Terbukti Benar.
Soal 8
Penyelesaian dari 6x + 8y = 21 dan 3x + 4y = 7 dengan metode eleminasi adalah...
A. 7 = 2
B. 1 = 7
C. 0 = 7
D. 7 = 1
E. 2 = 7
Jawaban : C. 0 = 7
pembahasan: 6x + 8y = 21 --> 6x + 8y = 21
3x + 4y = 7 --> 6x + 8y = 14 (persamaan kedua dikalikan dengan 2)
0 = 7
Soal 9
Jika diketahui m, n adalah kuadrat sempurna, maka terbuktik bahwa mn
adalah ...
A. bukan kuadrat sempurna
B. kuadrat sempurna
C. Konstanta
D. A dan C benar
E. Tidak ada jawaban yang benar
Jawaban : B. kuadrat sempurna
pembahasan: Misalkan m, n adalah kuadrat sempurna, artinya
m = k2, n = p2 untuk suatu k, p bilangan bulat.
mn = (k2)(p2)
= (kp)2
Karena k, p
Soal 10
Dibawah ini pernyataan yang benar tentang metode pembuktian langsung adalah ...
A. 3 adalah bilangan ganjil sebab terdapat 2
B. 4 adalah bilangan genap sebab terdapat 1
C. 5 adalah bilangan ganjil sebab terdapat 2
D. A, B, dan C benar
E. tidak ada jawaban yang benar
Jawaban : C. 5 adalah bilangan ganjil sebab terdapat 2
pembahasan: Suatu bilangan bulat n disebut bilangan GANJIL jika terdapat suatu bilangan bulat k, sehingga
n = 2k + 1.
5 = 2(2) + 1
5 = 4 + 1
5 = 5Soal 11
Jika diketahui n adalah ganjil, maka buktikan bahwa n2 adalah ganjil.
Jawaban dan pembahasan:
Diketahui n adalah ganjil, artinya terdapat suatu bilangan bulat k sehingga
n = 2k + 1. akan ditunjukkan bahwa n2 ganjil.
n2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) +1. Perhatikan bahwa
n2 = 2(2k2 + 2k) +1. karena k adalah bilangan bulat,
maka (2k2 + 2k) juga pasti bilangan bulat, sehingga n2 adalah ganjil.
Soal 12
Jika diketahui m, n adalah kuadrat sempurna, maka buktikan bahwa mn adalah juga kuadrat sempurna.
jawaban dan pembahasan:
Misalkan m, n adalah kuadrat sempurna, artinya m = k2, n = p2, untuk suatu k, p
suatu bilangan bulat. mn = (k2)(p2) = (kp)2 Karena k, p
Soal 13
Tunjukkan setidaknya ada 4 hari yang sama dari 22 hari.
Jawaban dan pembahasan:
Misal p = “setidaknya 4 dari 22 hari adalah hari yang sama” Andaikan –p bernilai benar, artinya paling banyak hanya ada 3 hari yang sama dari 22 hari. Ada 7 hari dalam sepekan, itu artinya paling banyak 21 hari bisa dipilih karena untuk setiap hari dalam sepekan, paling banyak tiga hari yang dipilih bisa jatuh pada hari itu. Ini kontradiksi dengan kenyataan bahwa kita memiliki 22 hari. Artinya jika r = “22 hari yang dipilih”, maka telah ditunjukkan bahwa –p (r -r). Artinya p bernilai benar
Soal 14
Gunakan induksi matematika untuk menunjukkan bahwa 5n – 1 habis dibagi 4 untuk semua bilangan bulat positif n.
Pembahasan dan jawaban
- Untuk n = 1,
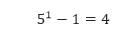
yang sangat jelas habis dibagi 4. - Kita anggap 5k – 1 habis dibagi 4 untuk sebarang bilangan bulat positif k. Akan kita tunjukkan 5k + 1 – 1 juga habis dibagi 4.
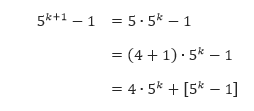
Karena 4 ∙ 5k dan 5k – 1 habis dibagi 4 maka 5k + 1 – 1 habis dibagi 4. Jadi, kita dapat menyimpulkan bahwa 5n – 1 habis dibagi 4 untuk semua bilangan bulat positif n.
Soal 15
Buktikan bahwa 32n – 1 habis dibagi 8 untuk semua bilangan bulat positif n.
Pembahasan dan jawaban:
Misalkan P(n) merupakan notasi untuk pernyataan “ 32n – 1 habis dibagi 8.”
- Pertama kita tunjukkan bahwa P(1) benar. Karena
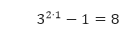
yang habis dibagi 8, maka P(1) terbukti benar. - Anggap bahwa P(k) benar. Sehingga hipotesis induksi kita menyatakan bahwa 32k – 1 habis dibagi 8. Selanjutnya kita akan tunjukkan bahwa P(k + 1) juga bernilai benar.
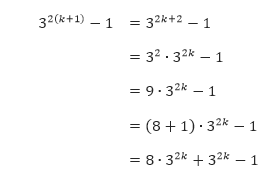
Karena 8 ∙ 32k dan 32k – 1 habis dibagi 8 maka 32(k + 1) – 1 habis dibagi 8. Jadi dengan menggunakan induksi matematika kita dapat menyimpulkan bahwa 32n – 1 habis dibagi dengan 8 untuk semua bilangan bulat positif n.
Soal 16
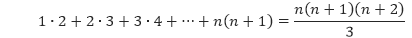
Buktikan bahwa n² – n + 41 merupakan bilangan ganjil untuk semua bilangan bulat positif n.
Pembahasan dan jawaban:
- Untuk n = 1,
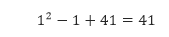
merupakan bilangan ganjil. - Kita anggap untuk sebarang bilangan bulat positif k, k² – k + 41 merupakan bilangan ganjil. Selanjutnya kita harus menunjukkan bahwa (k + 1)² – (k + 1) + 41 adalah bilangan ganjil.
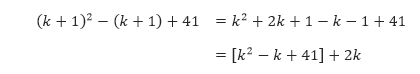
Karena k² – k + 41 adalah bilangan ganjil dan 2k adalah bilangan genap, maka jumlah kedua bilangan tersebut, yaitu (k + 1)² – (k + 1) + 41 merupakan bilangan ganjil. Jadi, dengan menggunakan Prinsip Induksi Matematika kita dapat meyimpulkan bahwa n² – n + 41 merupakan bilangan ganjil untuk semua bilangan bulat positif n.
Buktikan bahwa
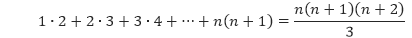
untuk semua bilangan bulat positif n.
Pembahasan dan jawaban:
Misalkan P(n) adalah pernyataan 1 ∙ 2 + 2 ∙ 3 + 3 ∙ 4 + … + n(n + 1) = [n(n + 1)(n + 2)]/3.
- Kita akan tunjukkan bahwa P(1) bernilai benar. Berdasarkan rumus di atas, P(1) menyatakan
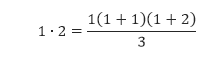
yang bernilai benar. - Anggap bahwa P(k) benar dan kita memperoleh hipotesis induksi sebagai berikut.
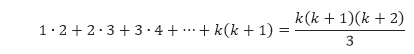
Hipotesis ini akan kita gunakan untuk membuktikan bahwa P(k + 1) benar. Pernyataan P(k + 1) menyatakan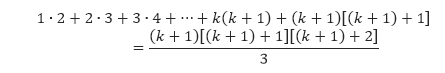
Kita mulai dari bentuk yang berada di ruas kiri, kemudian kita gunakan hipotesis induksi untuk mendapatkan bentuk pada ruas kanan.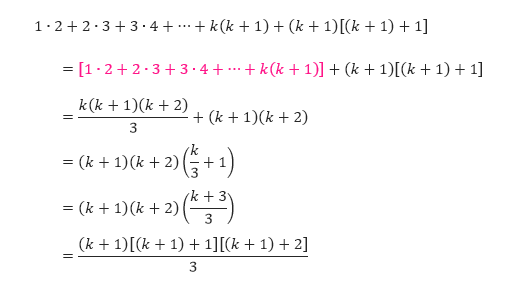
Sehingga kita telah menunjukkan bahwa P(k + 1) mengikuti P(k). Sehingga kita telah membuktikan langkah induksi.
Buktikan bahwa 4n < 2n untuk semua bilangan bulat positif n ≥ 5.
Pembahasan dan jawaban:
Misalkan P(n) menyatakan pernyataan 4n < 2n.
- P(5) adalah pernyataan 4 ∙ 5 < 25, atau 20 < 32, yang bernilai benar.
- Anggap P(k) benar. Sehingga hipotesis induksi kita adalah
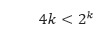
Kita akan menggunakan hipotesis ini untuk menunjukkan bahwa P(k + 1) benar, yaitu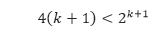
Sehingga kita mulai dengan bentuk di ruas kiri pertidaksamaan tersebut dan menggunakan hipotesis induksi untuk menunjukkan bahwa bentuk tersebut kurang dari bentuk yang berada di ruas kanan. Untuk k ≥ 5 kita mendapatkan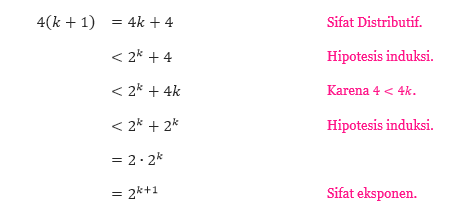
Sehingga P(k + 1) mengikuti P(k), sehingga kita telah melakukan langkah induksi.
Buktikan bahwa n! > 2n untuk semua bilangan bulat positif n ≥ 4.
Pembahasan dan jawaban:
Misalkan P(n) merupakan notasi untuk pernyataan n! > 2n.
- Pertama kita harus menunjukkan bahwa P(4) benar. Padahal P(4) menyatakan bahwa
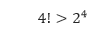
Karena 4! = 4 ∙ 3 ∙ 2 ∙ 1 = 24 dan 24 = 16, maka P(4) benar. - Kita anggap bahwa P(k): k! > 2k benar. Kita akan tunjukkan P(k + 1): (k + 1)! > 2k + 1 juga bernilai benar.
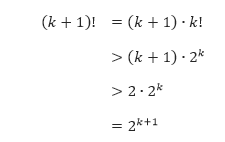
Sehingga pada langkah induksi ini kita dapat melihat bahwa kebenaran P(k) mengakibatkan P(k + 1). Jadi, dari Langkah 1 dan 2, kita dapat menyimpulkan dengan induksi matematika bahwa P(n) bernilai benar untuk n ≥ 4.
soal 20
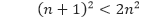
Buktikan bahwa
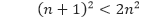
untuk semua bilangan bulat positif n ≥ 3.
Pembahasan dan jawaban:
Misalkan P(n) menyatakan (n + 1)² < 2n².
- Pernyataan P(3), yaitu
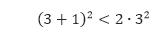
dengan jelas bernilai benar. - Anggap P(k): (k + 1)² < 2k² bernilai benar, kita harus menunjukkan bahwa P(k + 1) juga bernilai benar, yaitu [(k+1) + 1]² < 2(k + 1)². Untuk k ≥3, kita memperoleh
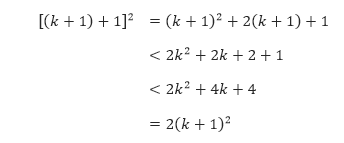
Sehingga kita telah menunjukkan kebenaran pernyataan jika P(k) benar maka P(k + 1). Oleh karena itu, berdasarkan Langkah 1 dan 2, dengan induksi matematika kita dapat menyimpulkan bahwa P(n) benar untuk semua bilangan bulat positif n ≥ 3.
DAFTAR PUSTAKA
https://youtu.be/jWUdt0ArwCQ
https://youtu.be/ptivxK4duyk



Tidak ada komentar:
Posting Komentar