Assalamualaikum wr.wb saya aliya rahmah XI IPS 2 akan memberikan contoh soal cerita dengan penyelesaian menggunakan invers dan determinan matriks.
1. Ani membeli 3 kg jeruk, 1 kg apel dan 1 kg alpukat dengan harga Rp61.000,00. Ida membeli 2 kg jeruk, 2 kg apel dan 1 kg alpukat dengan harga Rp67.000,00. Wati membeli 1 kg jeruk, 3 kg apel dan 2 kg alpukat dengan harga Rp80.000,00. Jika mereka bertiga membeli buah di toko yang sama, berapakah harga 1 kg dari masing-masing dari buah tersebut?
.Jawab
.Misal :
x = harga 1 kg jeruk
y = harga 1 kg apel
z = harga 1 kg alpukat
.
Bentuk sistem persamaan linear tiga variabelnya
3x + y + z = 61.000
2x + 2y + z = 67.000
x + 3y + 2z = 80.000
.
Bentuk matriksnya
A =
Kita tentukan matriks minornya
M =
C =
Adjoin A =
Untuk menentukan determinan A, kita gunakan cara kofaktor dengan baris 1
det A = a₁₁.C₁₁ + a₁₂.C₁₂ + a₁₃.C₁₃
det A = 3(1) + 1(-3) + 1(4)
det A = 4
maka
X = A⁻¹ . B
Jadi
harga 1 kg jeruk = Rp12.000,00
harga 1 kg apel = Rp18.000,00
harga 1 kg alpukat = Rp7.000,00
2. arman membeli 5 pensil dan 3 penghapus, sedangkan Susi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Arman membayar Rp 11.500,00 sedangkan Susi membayar Rp 9.000,00. Jika Dodi membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?
Persoalan ini dapat diselesaikan menggunakan dua cara.
Jika maka dengan cara pertama, yakni cara invers, diperoleh
.
Ingat, determinan dari adalah ad - bc.
Penyelesaian cara kedua adalah cara determinan, yaitu:
Penyelesaian
Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV)
5x + 3y = 11.500
4x + 2y = 9.000
Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni
Cara Pertama (Invers Matriks)
dan
Diperoleh harga satuan pensil Rp 2.000 dan harga satuan penghapus Rp 500.
Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500
-------------------------
Cara Kedua (Determinan Matriks)
Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500.
DAFTAR ISI
https://brainly.co.id/tugas/1476814















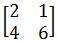
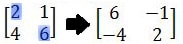
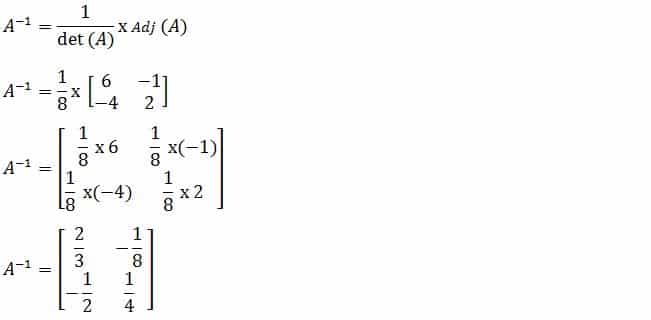
 Jawaban :
Jawaban :


