INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA DAN CONTOH SOAL

NAMA: ALIYA RAHMAH

KELAS: XI IPS 2

ABSEN: 04

INTEGRAL

 PENGERTIAN

Integral tak tentu dari suatu fungsi menghasilkan fungsi baru yang belum memiliki nilai yang tentu karena masih terdapat variabel dalam fungsi baru tersebut. Bentuk umum integral tentu .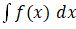

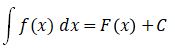
Rumus Integral Tak Tentu

Keterangan:

• f(x)  : persamaan kurva
• F(x)  : luasan di bawah kurva f(x)
• C     : konstanta

Contoh integral tak tentu:

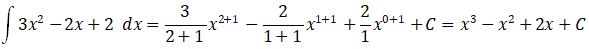
SIFAT INTEGRAL

Beberapa sifat integral yaitu sebagai berikut.

 

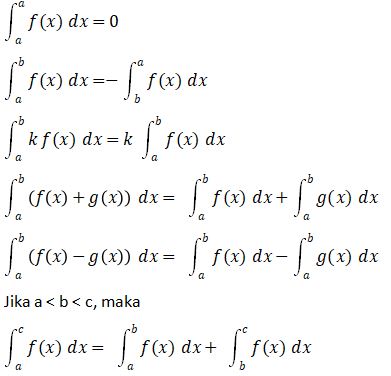
 CONTOH SOAL-SOAL INTEGRAL TAK TENTU

1. Tentukan hasil dari ʃ 3x² dx !

a. x³ + C.

b.2x² – 2x + C.

c.2x⁴ – 2x3

d.2x⁴ – 2x3

e.x³ + 8x² – 12x + C.

PEMBAHASAN:

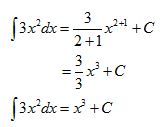
Jadi, hasil dari ʃ 3x² dx adalah x³ + C.

 

2. Carilah hasil integral tak tentu dari ʃ 8x³ – 6x² + 4x – 2 dx.

a. x³ + C.

b.2x² – 2x + C.

c.2x⁴ – 2x3

d. 2x⁴ – 2x³ + 2x² – 2x + C.

e.x³ + 8x² – 12x + C.

PEMBAHASAN:

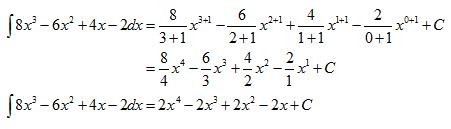
Jadi hasil dari ʃ 8x³ – 6x² + 4x – 2 dx adalah 2x⁴ – 2x³ + 2x² – 2x + C.

 

3. Carilah hasil integral tak tentu dari :

∫ 7 dx 

a. 7x + c 

b. 9x + c

c. 5x + c

e. 6x + d

 

PEMBAHASAN :

∫ k dx = kx + c

∫ 7 dx = 7x + c 

 

4. Carilah nilai integral berikut :

∫ (5 sin x + 2 cos x) dx 

a. x³ + 8x² – 12x + C.

b. 6x + d

c. -5cos x + 2sin x + c

d. x³ + 8x² – 12x + C.

e. -2sin x + 4cos x + 3 + c 

 

PEMBAHASAN:

∫ (5 sin x + 2 cos x) dx = -5cos x + 2sin x + c  

 

5. Carilah nilai integral berikut :

∫ (-2cos x - 4sin x + 3) dx 

a. x³ + 8x² – 12x + C.

b. 6x + d

c. 5cos x + 2sin x + c

d. x³ + 8x² – 12x + C.

e. -2sin x + 4cos x + 3 + c

PEMBAHASAN:

∫ (-2cos x - 4sin x + 3) dx = -2sin x + 4cos x + 3 + c 

 

6.  Tentukan nilai dari ʃ 4 sin x + 7 cos x dx !

a. – 4cos x + 7sin x + C.

b.2x² – 2x + C.

c.2x⁴ – 2x3

d. 2x⁴ – 2x³ + 2x² – 2x + C.

e.x³ + 8x² – 12x + C.

PEMBAHASAN:

ʃ sin x dx = – cos x + C

ʃ cos x dx = sin x + C

Maka:

ʃ 4 sin x + 7 cos x dx = – 4cos x + 7sin x + C

Jadi, nilai dari nilai dari ʃ 4 sin x + 7 cos x dx adalah – 4cos x + 7sin x + C.

 

7. Carilah nilai dari ʃ -5 sin x + 3 cos x – 4 dx!

a. – 4cos x + 7sin x + C.

b.2x² – 2x + C.

c.5 cos x + 3 sin x – 4 + C.

d. 2x⁴ – 2x³ + 2x² – 2x + C.

e.x³ + 8x² – 12x + C.

PEMBAHASAN:

ʃ sin x dx = – cos x + C

ʃ cos x dx = sin x + C

Maka:

ʃ -5 sin x + 3 cos x – 4 dx = (-5) ( -cos x) + 3 (sin x) – 4 + C

ʃ -5 sin x + 3 cos x – 4 dx = 5 cos x + 3 sin x – 4 + C

Jadi, nilai dari ʃ -5 sin x + 3 cos x – 4 dx adalah 5 cos x + 3 sin x – 4 + C.

 

 

DAFTAR PUSTAKA

https://rumuspintar.com/integral/ 

https://bfl-definisi.blogspot.com/2017/12/contoh-soal-integral-tak-tentu-beserta.html