PENGERTIAN TURUNAN DAN SIFAT-SIFATNYA BERSAMA CONTOH SOALNYA

NAMA: ALIYA RAHMAH 

KELAS: XI IPS 2 

ABSEN: 04

 

 PENGERTIAN TURUNAN

Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel). Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.

Menggunakan konsep limit yang sudah dipelajari, turunan dapat didefinisikan sebagai

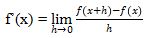
turunan tersebut didefinisikan sebagai limit dari perubahan rata-rata dari nilai fungsi terhadap variabel x

 

 SIFAT-SIFAT TURUNAN

1. Aturan Konstanta

   Jika f(x) = k dengan k suatu konstanta maka untuk sebarang x, f'(x) = 0 yakni D_x(k) = 0
   

2. Aturan Fungsi Identitas
   Jika f(x) = x maka f'(x) = 1 yakni D_x(x) = 1
   
3. Aturan Pangkat
   

   Jika f(x) = xⁿ, dengan n bilangan-bilangan bulat positif maka f(x) = nx^n-1 yakni D_x(xⁿ) = nx^n-1
   

4. Aturan Kelipatan Konstan
   

   Jika k suatu konstanta dan f suatu fungsi yang terdiferensial maka (kf)’ = k f'(x) yakni D_x[k f(x)] = k D_x[f(x)]
   

5. Aturan Jumlah
   

   Jika f dan g fungsi-fungsi yang terdiferensial maka (f + g)(x) = f(x) + g(x) yakni D_x[f(x) + g(x)] = D_x[f(x)] + D_x[g(x)]
   

6. Aturan Selisih
   

   Jika f dan g fungsi-fungsi yang terdiferensial maka (f – g)(x) = f(x) – g(x) yakni D_x[f(x) – g(x)] = D_x[f(x)] – D_x[g(x)]
   

7. Aturan Hasil Kali
   

   Jika f dan g fungsi-fungsi yang terdiferensial maka (f . g)'(x) = f'(x)g(x) + f(x)g'(x) yakni D_x[f(x)g(x)] = D_x[f(x)]g(x) + f(x)D_x[g(x)]
   

8. Aturan Hasil Bagi
   

   Jika f dan g fungsi-fungsi yang terdiferensial maka yakni D_x

    

   _{CONTOH SOAL:}

    _{1. Tentukan turunan dari fungsi berikut.}

   • f(x) = 8
   • g(x) = 3x + 5
   • h(x) = 6x³
   • k(x) = 3x^5/3
   • m(x) = (3x² + 3)⁴

   Pembahasan

   • f’(x) = 0
   • g’(x) = 3
   • h’(x) = 6 (3) x^{3 – 1} = 18x²
   • k’(x) = 3 (5/3) x^{(5/3) – 1} = 5x^2/3
   • m’(x) = 4 . (3x² + 3)^{4 – 1} . 6x = 24x . (3x² + 3)³
     

   _{2.Tentukan turunan dari fungsi berikut.}

   f(x) = (3x + 2) . (2x2 – 1)

   Pembahasan

   Misal: u(x) = 3x + 2 dan v(x) = 2x2 – 1

   f’(x) = u’(x) . v(x) + u(x) . v’(x)

   f’(x) = 3 . (2x2 – 1) + (3x + 2) . (4x)

   f’(x) = 6x2 – 3 + 12x2 + 8x = 18x2 + 8x – 3

   3. Diberikan sebuah fungsi ordo 2 seperti di bawah ini

   

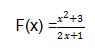
   Tentukan nilai f(0) + 3f’(1)

   Pembahasan

   Untuk mengerjakan soal ini, kita dapat memasukkan nilai 0 ke dalam fungsi tersebut.

   

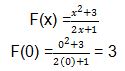
   Setelah Anda, mendapatkan nilai f(0). Kita dapat mengerjakan turunan fungsi hasil bagi menggunakan salah sifat turunan.

   

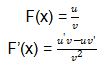
   Untuk menggunakan rumus tersebut, kita dapat menggunakan pemisalan dan turunannya seperti di bawah ini.

   U = x2 + 3 ; U’ = 2x

   V = 2x + 1 ; V’ = 2

   Kemudian, kita bisa memasukkan pemisalan tersebut ke dalam rumus turunan yang sebelumnya serta kita dapat secara langsung memasukkan f’x(1).

   

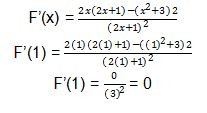
   Maka, hasil f(0) + 3f’(1) = 3 + 3(0) = 3

   4. Tentukan hasil turunan f(x) = (x2 + 2x + 3)(3x + 2)

   Pembahasan

   Sama seperti soal sebelumnya, Untuk mengerjakan soal turunan dalam bentuk perkalian, kita dapat menggunakan rumus sifat turunan serta menggunakan pemisalan dalam fungsi tersebut seperti di bawah ini.

   F’(x) = u’v + uv’

   U = x2 + 2x + 3 ; U’ = 2x + 3

   V = 3x + 2 ; V’ = 3

   F’(x) = u’v + uv’

   F’(x) = (2x+3)(3x + 2) + (x2 + 2x + 3)(3)

   F’(x) = 6x2 + 13x + 6 + 3x2 + 6x + 9

   F’(x) = 9x2 + 19x + 15

   Sehingga bentuk akhir F’(x) adalah 9x2 + 19x + 15

    5. Jika terdapat f(x) = (2x-1)2(x+2). Berapakah nilai f’x(2)

   Pembahasan

   Untuk mengerjakan soal ini, kita bisa menggunakan sifat turunan fungsi f’(x) = u’v + v’u untuk mendapatkan hasil akhir. Sehingga kita dapat melakukan pemisalan kembali.

   F’(x) = u’v + uv’

   U= (2x-1)2 = 4x2 – 4x + 1 ; U’ = 8x – 4

   V = x + 2 ; V’ = 1

   F’(x) = u’v + uv’

   F’(x) = (8x – 4)(x + 2) + (4x2 – 4x + 1)(1) ; kita dapat memasukkan nilai 2 seperti di soal

   F’(2) = ((8(2) – 4)(2 + 2)) + ((4(2)2 – 4(2) + 1)(1))

   F’(2) = ((16-4)(4)) + ((16-8+1)(1))

   F’(2) = 96 + 9 = 105

   Sehingga nilai akhir F’(2) adalah 105

    

   _6. Turunan pertama dari f(x)=4x−3−6x adalah f′(x). Nilai dari f′(1) adalah ⋯⋅

   A. −5                 C. 4                 E. 10
   B. 2                    D. 5

   Pembahasan

   Gunakan aturan turunan dasar untuk mencari turunan pertama dari fungsi f(x).
   f(x)=4x−3−6x=4(x−3⏟u)−1−6x−1f′(x)=4(−1)(x−3)−2⋅1⏟u′−6(−1)x−2=−4(x−3)2+6x2Substitusi x=1 dan kita akan peroleh
   f′(1)=−4((1)−3)2+6(1)2=−44+61=−1+6=5
   Jadi, nilai dari f′(1)=5
   (Jawaban D)

    

    

    

    _{DAFTAR PUSTAKA}

    _{https://aimprof08.wordpress.com/2012/05/02/turunan-dan-sifat-sifatnya/}

   _{https://rumuspintar.com/turunan/} 

   
   

SIFAT SIFAT LIMIT DAN CONTOH SOAL SERTA SOAL KONTEKSTUAL

Nama: Aliya Rahmah

Kelas: XI IPS 2

Absen 04

Sifat Limit Fungsi Aljabar

Jika n adalah bilangan bulat positif, k konstanta, f dan g merupakan fungsi yang memiliki limit di c, maka sifat-sifat di bawah ini berlaku.

Contoh Soal

Berikut ini adalah beberapa contoh soal agar memudahkan dalam memahami limit fungsi aljabar

Soal No. 1
Tentukanlah nilai fungsi limit dari:

Jawab :
Limit bentuk

di dapat

Soal No. 2

Pembahasan
Limit aljabar bentuk

Substitusikan saja nilai x,
 

contoh soal kontekstual

1. Angka pertumbuhan penduduk setiap tahun dirumuskan dengan p(t)=√12t2−3t+5 dengan p(t) dalam persen dan t dalam tahun. Pertumbuhan penduduk mendekati tahun kelima (t=5) adalah ⋯%.

Pembahasan:

Secara matematis, angka pertumbuhan penduduk saat t mendekati tahun ke-5 adalah limt→5p(t).
Diketahui p(t)=√12t2−3t+5.
Dengan menggunakan teknik substitusi, kita peroleh
limt→5√12t2−3t+5=√12(5)2−3(5)+5=√252−10=√12,5−10=√2,5
Jadi, angka pertumbuhan penduduk akan mendekati √2,5%

 2.Diketahui limx→af(x)=m. Jika f(x)=2x, maka nilai dari limx→af(x2−1)=⋯⋅

Sebuah mobil bergerak dengan kecepatan sesaat (instantaenous velocity) yang dirumuskan dengan v(t)=t2−t dengan v(t) dalam meter dan t dalam detik. Jika t mendekati 5 detik, maka kecepatan mobil tersebut adalah ⋯ m/detik.
A. 10                  C. 15                E. 25
B. 12                  D. 20

Pembahasan

Secara matematis, kecepatan mobil saat t mendekati detik ke-5 adalah limx→5v(t).
Diketahui v(t)=t2−t.
Dengan menggunakan teknik substitusi, kita peroleh
limx→5(t2−t)=(5)2−(5)=25−5=20
Jadi, kecepatan mobil akan mendekati 20 m/detik.

 

 

 

Daftar Pustaka 

https://rumus.co.id/limit-fungsi-aljabar/