SOAL TRANSFORMASI GEOMETRI(DILATASI,REFLEKSI,ROTASI,TRANSLASI DENGAN MATRIKS)

 

 ASSALAMUALAIKUM WR.WB ALIYA RAHMAH XI IPS 2 

SOAL DAN PEMBAHASAN TRANSFORMASI GEOMETRI DENGAN MATRIKS

1. T₁ dan T₂ adalah transformasi yang masing-masing bersesuaian dengan 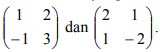Ditentukan T = T₁ o T₂ , maka transformasi T bersesuaian dengan matriks…

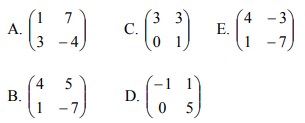
Jawaban : E

Pembahasan : 

2.. Ditentukan matriks transformasi .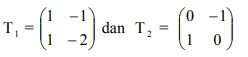 Hasil transformasi titik (2,-1) terhadap T₁ dilanjutkan T₂ adalah…. 

A. (-4,3)

B. (-3,4)

C. (3,4)

D. (4,3)

E. (3,-4)

Jawaban : A

Pembahasan : 

 

3.  Persamaan bayangan garis y = -6x + 3 karena transformasi oleh matriks  kemudian dilanjutkan dengan matriks 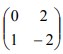adalah…

A. x + 2y + 3 = 0 

B. x + 2y – 3 = 0 

C. 8x – 19y + 3 = 0

D. 13x + 11y + 9 = 0

E. 13x + 11y – 9 = 0

Jawaban : E

Pembahasan : 

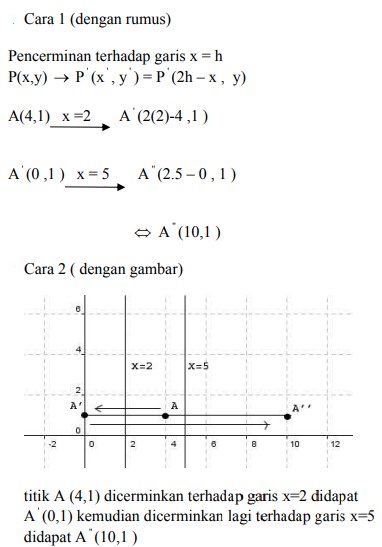
4. Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik…. 

A. A” (8,5) 

B. A” (10,1)

C. A” (8,1) 

D. A” (4,5)

E. A” (20,2)

Jawaban : B

Pembahasan : 

5. T₁ adalah transformasi yang bersesuaian dengan matriks 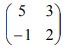dan T₂ adalah transformasi yang bersesuaian dengan matriks 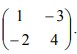Bayangan A (m,n) oleh transformasi T₁ o T₂ adalah (-9,7). Nilai m+n sama dengan…

A. 4

B. 5

C. 6

D. 7

E. 8 

Jawaban : B

Pembahasan : 

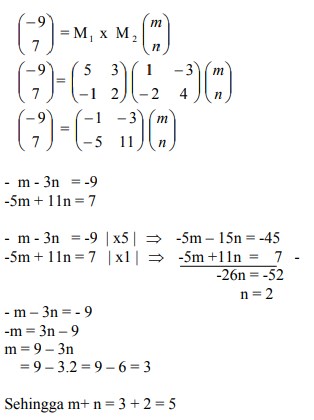
6. Bayangan ∆ABC dengan A(2,1), B(6,1), C(5,3) karena refleksi terhadap sumbu y dilanjutkan rotasi (0,90°) adalah…

A. A” (-1,-2), B” (1,6) dan C” (-3,-5)

B. A” (-1,-2), B” (1,-6) dan C” (-3,-5)

C. A” (1,-2), B” (-1,6) dan C” (-3,5)

D. A” (-1,-2), B” (-1,-6) dan C” (-3,-5)

E. A” (-1,2), B” (-1,-6) dan C” (-3,-5)

Jawaban : D

Pembahasan : 

7. Persamaan peta kurva y = x² – 3x + 2 karena pencerminan terhadap sumbu x dilanjutkan dilatasai dengan pusat O dan factor skala 3 adalah…

A. 3y + x² – 9x + 18 = 0

B. 3y – x² + 9x – 18 = 0

C. 3y – x² + 9x + 18 = 0

D. 3y + x² + 9x + 18 = 0

E. y + x² + 9x – 18 = 0 

Jawaban : A

Pembahasan : 

pencerminan terhadap sumbu x:

P ( x , y ) → P ‘ ( x , – y )

Dilatasi terhadap titik pusat O(0,0) dengan factor skala 3 :

[O, k] : P(x,y) → P'(kx, ky)

[O,3k] : P(x,y) → P'(3x, 3y)

pencerminan terhadap sumbu x dilanjutkan dilatasai
dengan pusat O dan factor skala 3 :

P(x,y) → P ‘(x, -y) → P ”(3x, -3y)

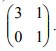8. Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi Luas bangun hasil transformasi segitiga ABC adalah….

A. 56 satuan luas 

B. 36 satuan luas

C. 28 satuan luas

D. 24 satuan luas 

E. 18 satuan luas

Jawaban : E

Pembahasan : 

misalkan T = 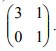maka

Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3

luas ∆ ABC :

buat sketsa gambar :

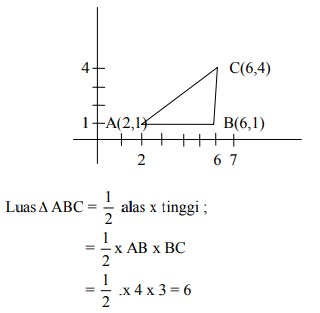
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC

= 3 x 6 = 18 satuan luas

 

DAFTAR PUSTAKA

 https://soalkimia.com/contoh-soal-transformasi-geometri/

transformasi, Refleksi, Rotasi, dan Dilatasi dengan gambar balok

assalamualaikum wr.wb saya aliya rahmah XI ips 2 absen 03 akan membahas Transformasi Translasi, Refleksi, Rotasi dan Dilatasi dengan gambar balok ABCDEFGH koordinat titik A(0,0), B(4,0), C(4,4), D(0,4), E(10,0), F(14,0), G(14,4), H(10,4) dan perhitungan mendapat bayangannya.

 

1. Transformasi atau nama lengkapnya Transformasi Geometri adalah perubahan posisi atau perpindahan dari posisi awal P(x, y) ke posisi lain P'(x', y'). Nah perubahan posisi ini bisa disebabkan oleh 4 hal:

1. Translasi atau pergeseran
2. Refleksi atau pencerminan
3. Rotasi atau perputaran
4. Dilatasi atau perkalian yang mengakibatkan bidang geometri mengalami perbesaran atau pengecilan.

a. Translasi atau pergeseran adalah bentuk transformasi geometri yang tidak mengubah bentuk dan ukuran, hanya mengubah posisi ke kiri, kanan, atas dan atau bawah.

Beberapa hal yang perlu diingat tentang konsep translasi yaitu:

• Pergeseran ke kanan atau ke kiri hanya mempengaruhi variabel x
• Pergeseran ke atas atau ke bawah hanya mempengaruhi variabel y
• Pergeseran ke kanan atau atas tandanya negatif (-)
• Pergeseran ke kiri atau bawah tandanya positif (+).

Ingat saja diagram kartesius :)

Rumus praktis translasi oleh T(a, b) adalah

b. Pencerminan atau refleksi adalah salah satu jenis transformasi geometri yang akan memetakan suatu titik pada bangun geometri dengan menggunaan sifat benda dan bayangan pada cermin datar. Bayangan hasil pencerminan akan memiliki bentuk dan ukuran yang sama dengan bentuk dan ukuran awalnya.

Rumus Pencerminan Terhadap Sumbu X:

Rumus Pencerminan Terhadap Sumbu Y:

Rumus Pencerminan Terhadap Titik Pusat O(0, 0):

Rumus Pencerminan Terhadap Titik (a, b):

Rumus Pencerminan Terhadap Garis x = y:

Rumus Pencerminan Terhadap Garis x = -y atau -x = y:

Rumus Pencerminan Terhadap Garis x = a:

Rumus Pencerminan Terhadap Garis y = a:

c. Dilatasi : Perbesaran atau pengecilan suatu objek berdasarkan skala yang telah ditentukan. Dalam geometri transformasi, dilatasi dapat dirumuskan dengan perkalian matriks.

A adalah titik (Ax,Ay), P adalah pusat titik (Px,Py), dan S adalah faktor skala.

A' =  ( S 0 ) ( Ax-Px ) + ( Px )

     ( 0 S ) ( Ay-Py )   ( Py )

Dilatasi menurut jenis skalanya dibagi menjadi dua, yaitu dilatasi pembesaran (dimana S>1) dan pengecilan (dimana 0<S<1).

d. Rotasi (perputaran) :  Perputaran suatu objek dengan bertumpu pada suatu titik pusat sejauh nilai derajatnya yaitu 0 sampai 360 derajat. Dalam geometri transformasi, rotasi dapat dirumuskan dengan perkalian dan penjumlahan matriks.

A adalah titik (Ax,Ay), P adalah matriks untuk rotasi dengan menggunakan rumus trigonometri yaitu sin dan cos, dan α adalah besarnya sudut suatu rotasi yang dinyatakan dengan derajat (°). Rumus ini berlaku selama titik pusatnya adalah O (0,0).

A' = P * A = ( cos α  sin α )  ( Ax )

                  ( -sin α  cos α ) ( Ay )

Rotasi dapat dibagi menjadi 2, yaitu arah jarum jam (ke kanan) dengan nilai positif dan berlawanan arah jarum jam (ke kiri) dengan nilai negatif. 

 

 

GAMBAR KOORDINAT BALOK 

PERHITUNGAN TRANSLASI, DILATASI, REFLEKSI, 

 ROTASI

SOAL CERITA INVERS MATRIKS DAN DETERMINAN

Assalamualaikum wr.wb saya aliya rahmah XI IPS 2 akan memberikan contoh soal cerita dengan penyelesaian menggunakan invers dan determinan matriks.

1. Ani membeli 3 kg jeruk, 1 kg apel dan 1 kg alpukat dengan harga Rp61.000,00. Ida membeli 2 kg jeruk, 2 kg apel dan 1 kg alpukat dengan harga Rp67.000,00. Wati membeli 1 kg jeruk, 3 kg apel dan 2 kg alpukat dengan harga Rp80.000,00. Jika mereka bertiga membeli buah di toko yang sama, berapakah harga 1 kg dari masing-masing dari buah tersebut?

.Jawab

.Misal  :

x = harga 1 kg jeruk

y = harga 1 kg apel

z = harga 1 kg alpukat

.

Bentuk sistem persamaan linear tiga variabelnya

3x + y + z = 61.000

2x + 2y + z = 67.000

x + 3y + 2z = 80.000

.

Bentuk matriksnya

A =  

Kita tentukan matriks minornya

M =  

C =  

Adjoin A =  

Untuk menentukan determinan A, kita gunakan cara kofaktor dengan baris 1

det A = a₁₁.C₁₁ + a₁₂.C₁₂ + a₁₃.C₁₃

det A = 3(1) + 1(-3) + 1(4)

det A = 4

maka

X = A⁻¹ . B

Jadi  

harga 1 kg jeruk = Rp12.000,00

harga 1 kg apel = Rp18.000,00

harga 1 kg alpukat = Rp7.000,00 

2. arman  membeli 5 pensil dan 3 penghapus, sedangkan Susi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Arman membayar Rp 11.500,00 sedangkan Susi membayar Rp 9.000,00. Jika Dodi membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?

Persoalan ini dapat diselesaikan menggunakan dua cara.

Jika maka dengan cara pertama, yakni cara invers, diperoleh .

Ingat, determinan dari adalah ad - bc.

Penyelesaian cara kedua adalah cara determinan, yaitu:

Penyelesaian

Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV)

5x + 3y = 11.500

4x + 2y = 9.000

Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni

Cara Pertama (Invers Matriks)

 

 

 

dan

Diperoleh harga satuan pensil Rp 2.000 dan harga satuan penghapus Rp 500.

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500

-------------------------

Cara Kedua (Determinan Matriks)

Jadi, Dodi harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500.

DAFTAR ISI

 https://brainly.co.id/tugas/1476814