program linear

assalamualaikum wr.wb 
saya aliya rahmah XI IPS 2 ingin memberikan materi-materi program linear.

Program Linear 

A. PENDAHULUAN 
 Program linear adalah suatu program untuk menyelesaikan permasalahan yang batasbatasannya berbentuk sistem pertidaksamaan linear dua variabel (SPTLDV).   
Program linear mempelajari empat hal utama: 
1) Menggambar daerah penyelesaian (DP) dari PTLDV atau SPTLDV. 
2) Menentukan PTLDV atau SPTLDV dari daerah penyelesaian. 
3) Menentukan nilai optimum (nilai maksimum dan minimum) pada daerah penyelesaian. 
4) Menyelesaikan masalah mengenai optimasi yang berkaitan dengan program linear. 

B. MENENTUKAN DAERAH PENYELESAIAN 
 Daerah penyelesaian merupakan himpunan penyelesaian (nilai benar) dari PTLDV atau SPTLDV.  Daerah penyelesaian dapat dibuktikan melalui pendekatan grafik pada bidang kartesius.  
Langkah menentukan DP: 
1) Tentukan dua buah titik sembarang dari pertidaksamaan. 
2) Tarik garis sehingga kedua titik terhubung dan membagi bidang kartesius menjadi dua bagian. 
3) Periksa/uji nilai titik di salah satu bagian yang telah terbagi tadi, dengan memasukkan nilai x dan y titik ke pertidaksamaan. 
4) Jika daerah yang terdapat titik yang diuji nilainya bernilai benar, maka itulah daerah penyelesaian. Jika tidak, maka daerah penyelesaiannya berada di bidang lawannya. 
5) Jika pertidaksamaan mempunyai sama dengan, maka titik-titik pada garis juga merupakan daerah penyelesaian. Jika pertidaksamaan tidak mempunyai sama dengan, maka titik-titik pada garis bukan daerah penyelesaian.
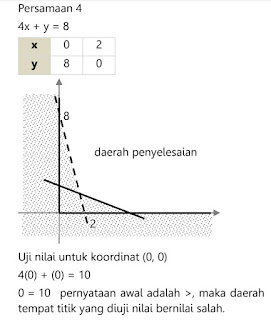
 Contoh: Tentukan daerah penyelesaian dari SPTLDV berikut ini:
 x ≥ 0 …(1) 
y ≥ 0 …(2) 
2x + 5y ≥ 10 …(3) 
4x + y > 8 … (4) 

C. PERSAMAAN GARIS  
Persamaan garis dapat dibentuk dari suatu garis pada bidang kartesius. 

 D. MENENTUKAN SPTLDV DARI DAERAH PENYELESAIAN 
 Cara menentukan PTLDV dan SPTLDV dari grafik daerah penyelesaian: 
1) Jumlah garis pembatas daerah penyelesaian adalah jumlah SPTLDV. 
2) Tentukan semua persamaan garis dengan rumus-rumus pada pembahasan sebelumnya. 
3) Uji nilai titik di salah satu bagian yang dibagi garis untuk menentukan tanda pertidaksamaan yang tepat. 
Contoh: Tentukan pertidaksamaan-pertidaksamaan yang memenuhi daerah penyelesaian berikut ini!

Garis 1
 -4x + 8y  = -4. 8    
 x – 2y      = 8
 Uji titik koordinat untuk (0, 0) (daerah benar)
 (0) – 2(0) = 8 0 = 8, 
tandanya adalah ≤ dan titik berada di daerah benar,
 maka x – 2y ≤ 8 

Garis 2 (tegak lurus dengan garis 1) Tentukan titik potongnya terlebih dahulu dengan garis 1 (diketahui x = 12)      
 x - 2y   = 8   
 12 – 2y = 8           
   y         = 2 
berpotongan pada (12, 2), 
maka  2x + y = 2. 12 + 1. 2   
   2x + y = 26
 Uji titik koordinat untuk (0, 0) (daerah benar) 2(0) + (0) = 26
 0 = 26, tandanya adalah ≤ dan titik berada di daerah benar, 
maka 2x + y ≤ 26

Garis 3 (berpotongan dengan garis 2) 
Tentukan titik potongnya dengan garis 2 (diketahui y = 12)       
2x + y  = 26    
 2x + 12  = 26              
 x  = 7 berpotongan pada (7, 12), dan ada titik pada 0, 0, 
maka 12x + 7y = 0 
Uji titik koordinat untuk (1, 0) (daerah benar) 
12(1) + 7(0) = 0 12 = 0, tandanya adalah ≥ dan titik berada di daerah benar,
 maka 12x + 7y ≥ 0

Garis 4     
3x + 4y = 4. 3    
 3x + 4y = 12 Uji titik koordinat untuk (0, 0) (daerah salah)
 3(0) + 4(0) = 12 0 = 12, tandanya adalah ≤ dan titik berada di daerah salah,
 maka 3x + 4y ≥ 12 E

contoh soal

1.    Nilai maksimum f(x, y) = 5x + 4y yang memenuhi pertidaksamaan x + y ≤ 8, x + 2y ≤ 12, x ≥ 0, dan y ≥ 0 adalah ...
a.    24
b.    32
c.    36
d.    40
e.    60
PEMBAHASAN:
-    x + y ≤ 8
ketika x = 0, maka y = 8 .... (0, 8)
ketika y = 0, maka x = 8 .... (8, 0)
-    x + 2y ≤ 12
ketika x = 0, maka y = 6 .... (0, 6)
ketika y = 0, maka x = 12 .... (12, 0)
Sehingga, grafik dari pertidak samaan di atas adalah:

Kita cari dulu titik B, yaitu titik potong dua buah garis, yaitu:

subtitusikan y = 4 dalam x + y = 8
x + 4 = 8
x = 4 .... (4, 4)
Jadi, nilai fungsi obyektifnya adalah:
f(x, y) = 5x + 4y
-    titik A (0, 6)
      5x + 4y = 5.0 + 4.6 = 24
-    titik B (4, 4)
      5x + 4y = 5.4 + 4.4 = 20 + 16 = 36
-    titik C (8, 0)
      5x + 4y = 5.8 + 4.0 = 40
Jadi, nilai maksimumnya adalah 40.
JAWABAN: D

2.    Nilai minimum fungsi obyektif  f(x, y) = 3x + 2y dari daerah yang diarsir pada gambar adalah  ...

a.    4
b.    6
c.    7
d.    8
e.    9
PEMBAHASAN:
Perhatikan gambar berikut:

Ingat ya, rumus persamaan garis yang melalui titik (0, a) dan (b, 0) adalah: ax + by = a.b, maka:
-    Persamaan garis p = 4x + 2y = 4.2 = 4x + 2y = 8 = 2x + y = 4
-    Persamaan garis q = 3x + 3y = 3.3 = 3x + 3y = 9 = x + y = 3
Selanjutnya, kita cari titik potong garis p dan q, yaitu di titik B:

subtitusikan x = 1 dalam x + y =3
1 + y = 3
y = 2 .... B(1, 2)
kita cari nilai dari fungsi obyektif  f(x, y) = 3x + 2y:
-    Titik A (0, 4)
     3x + 2y = 3.0 + 2.4 = 8
-    Titik B (1, 2)
      3x + 2y = 3.1 + 2.2 = 7
-    Titik C (3, 0)
      3x + 2y = 3.3 + 2.0 = 9
Jadi, nilai minimumnya adalah 7
JAWABAN: C

3.    Daerah yang merupakan himpunan penyelesaian dari pertidaksamaan 2x + 3y ≤ 12, 4x + y ≥ 10, x ≥ 0, y ≥ 0 adalah ...

a.    I
b.    II
c.    III
d.    IV
e.    I dan III
PEMBAHASAN:
-    Daerah hasil 2x + 3y ≤ 12 adalah area II dan III
-    Daerah hasil  4x + y ≥ 10 adalah area III dan IV
Maka, yang mencakup keduanya adalah area nomor III
JAWABAN: C

  4.    Daerah mana yang diarsir di bawah ini adalah daerah penyelesaian suatu sistem pertidaksamaan. Nilai maksimum fungsi objektif (3x + 5y) pada daerah penyelesaian tersebut ...

a.    30
b.    26
c.    24
d.    21
e.    18
PEMBAHASAN:
Perhatikan gambar:

-    Persamaan garis p = 6x + 4y = 24 atau 3x + 2y = 12
-    Persamaan garis q = 4x + 6y = 24 atau 2x + 3y = 12
Titik potong garis p dan q adalah:

subtitusikan y = 12/5 dalam 2x + 3y = 12:
2x + 3.12/5 = 12
2x = 12 – 36/5
2x = 60/5 – 36/5
2x = 24/5
x = 24/10 = 12/5 .... titik B (12/5, 12/5)
Nilai dari fungsi obyektif  3x + 5y adalah:
-    Titik A (0, 6)
      3x + 5y = 3.0 + 5. 6 = 30
-    Titik B (12/5, 12/5)
      3x + 5y = 3.12/5 + 5.12/5 = 36/5 + 60/5 = 96/5 = 19,2
-    Titik C (6, 0)
      3x + 5y = 3.6 + 5.0 = 18
Jadi, nilai minimumnya adalah 18
JAWABAN: E

5. Nilai maksimum dari z = -3x + 2y yang memenuhi syarat 3x + y ≤ 9, 5x + 4y ≥ 20, x ≥ 0 adalah ...
a.    10
b.    14
c.    18
d.    20
e.    24
PEMBAHASAN:
-    3x + y ≤ 9
Jika x = 0, maka y = 9 .... (0, 9)
Jika y = 0, maka x = 3 .... (3, 0)
-    5x + 4y ≥ 20
Jika x = 0, maka y =5 ..... (0, 5)
Jika y = 0, maka x = 4 .... (4, 0)
Kita cari daerah hasilya dengan menggambarnya:

Kita cari dulu titik potong kedua garis di titik B:

subtitusikan x = 16/7 dalam 3x + y = 9
3.16/7 + y = 9
48/7 + y = 9
y = 9 – 48/7
y = 63/7 – 48/7
y = 15/7 ... titik B (16/7, 15/7)
Kita cari nilai dari fungsi obyektif  z = -3x + 2y:
-    Pada titik A (0, 9)
      -3x + 2y = -3.0 + 2.9 = 18
-    Pada titik B (16/7, 15/7)
     -3x + 2y = -3.16/7 + 2.15/7 = -48/7 + 30/7 = -18/7
-    Pada titik C (0, 5)
     -3x + 2y = -3.0 + 2.2 = 4
Jadi, nilai maksimumnya adalah 18.
JAWABAN: C

DAFTAR PUSTAKA

https://materi78.wordpress.com