MATRIKS, MACAM MACAM MATRIKS DAN OPERASI MATRIKS

 assalamualaikum, saya aliya rahmah xi ips 2 akan membahas materi matriks

MATRIKS

Matriks adalah sekumpulan bilangan yang disusun secara baris dan kolom, dan ditempatkan   dalam kurung biasa atau kurung siku. Bilangan-bilangan pembentuk matriks disebut elemen-    elemen matriks.

 Contoh: 

A = (4 5 3 -1)  

B = (6 2 -4 0 9 10)  

KOMPONEN-KOMPONEN MATRIKS

1) Elemen Elemen adalah bilangan-bilangan yang menyusun suatu matriks, ditulis dalam tanda kurung. 

2) Baris dan kolom Baris adalah susunan elemen yang ditulis mendatar/horizontal. Kolom adalah susunan elemen yang ditulis menurun/vertikal.

 

3) Ordo Ordo menyatakan banyak baris (m) diikuti banyak kolom (n). Ordo matriks = m x n

4) Diagonal Diagonal matriks terdapat pada matriks persegi, yaitu diagonal utama dan diagonal samping. 

 

 

 

JENIS-JENIS MATRIKS

Matriks berdasarkan ukuran dibagi menjadi: 

         1) Matriks baris 

             A = (a b c)

 

OPERASI HITUNG MATRIKS 

>Penjumlahan dan pengurangan matriks dapat dilakukan pada matriks berordo sama.

>Penjumlahan dan pengurangan matriks dilakukan dengan menjumlah atau mengurang elemenelemen seletak matriks yang dioperasikan. 

>Sifat penjumlahan dan pengurangan matriks adalah komutatif A x B = B+A

>perkalian matriks dengan suatu bilangan dioperasikan dengan:

>perkalian matriks dapat dilakukan pada matriks berordo m x n dengan ordo n x p (jumlah kolom      matriks 1 = jumlah baris matriks 2)

>perkalian matriks berordo m x n dengan ordo n x p menghasilkan matriks berordo m x p.

DAFTAR PUSTAKA

materi78.wordpress.com

buku matematika PKS halaman 34-62

SOAL NILAI OPTIMUM MENENTUKAN LABA

 soal

SAYA ALIYA RAHMAH XI IPS 2 AKAN MENJAWAB SOAL BERIKUT

1. persediaan kain 20 meter dan kain bergaris 10 meter Dewi akan membuat 2 model pakaian jadi. Model I memerlukan tidak lebih dari 1 m kain polos dan 1,5 m kain bergaris. Model II memerlukan tidak lebih dari 2 m kain polos dan 0,5 m kain bergaris. Bila pakaian tersebut dijual, setiap model I memperoleh untung tidak kurang dari Rp. 15.000,00 dan model II memperoleh untung tidak kurang dari  Rp. 10.000,00. Laba yang diperoleh Dewi adalah sebanyak ….

JAWABAN DAN PEMBAHASAN:

 

           

 

jadi laba yang dihasilkan oleh dewi ialah Rp. 140.000

SOAL CERITA MENENTUKAN NILAI OPTIMUM PROGRAM LINEAR

ASSALAMUALAIKUM WR.WB SAYA ALIYA RAHMAH XI IPS 2 AKAN MEMBERIKAN CONTOH SOALCERITA MENENTUKAN NILAI OPTIMUM DAN PEMBAHASANNYA.

 

CONTOH SOAL 

 

1. Nilai optimum dari z = -3x + 2y yang memenuhi syarat 3x + y ≤ 9, 5x + 4y ≥ 20, x ≥ 0 adalah ...
a.    10
b.    14
c.    18
d.    20
e.    24
PEMBAHASAN:
-    3x + y ≤ 9
Jika x = 0, maka y = 9 .... (0, 9)
Jika y = 0, maka x = 3 .... (3, 0)
-    5x + 4y ≥ 20
Jika x = 0, maka y =5 ..... (0, 5)
Jika y = 0, maka x = 4 .... (4, 0)
Kita cari daerah hasilya dengan menggambarnya:

Kita cari dulu titik potong kedua garis di titik B:

subtitusikan x = 16/7 dalam 3x + y = 9
3.16/7 + y = 9
48/7 + y = 9
y = 9 – 48/7
y = 63/7 – 48/7
y = 15/7 ... titik B (16/7, 15/7)
Kita cari nilai dari fungsi obyektif  z = -3x + 2y:
-    Pada titik A (0, 9)
      -3x + 2y = -3.0 + 2.9 = 18
-    Pada titik B (16/7, 15/7)
     -3x + 2y = -3.16/7 + 2.15/7 = -48/7 + 30/7 = -18/7
-    Pada titik C (0, 5)
     -3x + 2y = -3.0 + 2.2 = 4
Jadi, nilai optimumnya adalah 18.
JAWABAN: C

2.  Dalam sistem pertidaksamaan: 2y ≥ x : y ≤ 2x; 2y + x ≤ 20; x + y ≥ 9. Nilai optimum untuk 3y – x dicapai di titik ...

a.    P
b.    Q
c.    R
d.    S
e.    T
PEMBAHASAN:
Kita cari dulu titik potong-titik potong pada soal di atas:
-    Titik P
P adalah perpotongan dari x + y = 9 dan 2y = x, maka subtitusikan saja:
2y + y = 9
3y = 9
y = 3 maka x = 2y = 6 ... titik P (6, 3)
Nilai obyektifnya: 3y – x = 3.3 – 6 = 3
-    Titik Q
Q adalah perpotongan dari x + y = 9 dan y = 2x, maka subtitusikan saja:
x + 2x = 9
3x = 9
x =3 dan y = 2x = 6 ... titik Q(3, 6)
Nilai obyektifnya: 3y – x = 3.6 – 3 = 15
-    Titik R
R adalah perpotongan dari 2y + x = 20 dan y = 2x, maka subtitusikan saja:
2.2x + x = 20
5x = 20
x = 4 dan y = 2x = 8 ... titik R (4, 8)
Nilai obyektifnya: 3y – x = 3.8 – 4 = 20
-    Titik S
S adalah perpotongan dari 2y + x = 20 dan 2y = x, maka subtitusikan saja:
x + x = 20
2x = 20
x = 10 dan 2y = x, maka y = 5 ... titik S (10, 5)
Nilai obyektifnya: 3y – x = 3.5 – 10 = 5
Maka, nilai optimumnya adalah 20 di titik R
JAWABAN: C

3. Fungsi F = 10x + 15y dengan syarat x ≥ 0, y ≥ 0, x ≤ 800, y ≤ 600, dan x + y ≤ 1000 mempunyai nilai maksimum ...
a.    9.000
b.    11.000
c.    13.000
d.    15.000
e.    16.000
PEMBAHASAN:
-    x = 800
-    y = 600
-    x + y = 1000
     jika x = 0, maka y = 1000 ... (0, 1000)
     jika y = 0, maka x= 1000 ... (1000, 0)
Yuk, kita gambar daerah hasilnya:

-    titik A adalah titik potong antara y = 600 dan x + y = 1000, maka titik A adalah:
x + 600 = 1000
x = 400 ... titik A (400, 600)
Maka nilai obyektif  F = 10x + 15y adalah: 10.400 + 15.600 = 4000 + 9000 = 13.000
-    titik B (0, 600)
Maka nilai obyektif  F = 10x + 15y adalah: 10.0 + 15.600 = 0 + 9000 = 9.000
-    titik C adalah titi potong antara x = 800 dan x + y = 1000, maka titik C adalah:
800 + y = 1000
y = 200 .... titik C (800, 200)
Maka nilai obyektif  F = 10x + 15y adalah: 10.800 + 15.200 = 8000 + 3000 = 11.000
-    titik D (800, 0)
Maka nilai obyektif  F = 10x + 15y adalah: 10.800 + 15.0 = 8000 + 0 = 8.000
Sehingga nilai maksimumnya adalah 13.000
JAWABAN: C

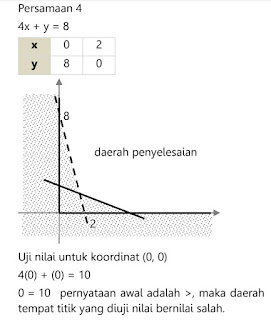
4. Nilai minimal dari z = 3x + 6y yang memenuhi syarat;4x + y ≥ 20, x + y ≤ 20, x + y ≥ 10, x ≥ 0, dan y ≥ 0 adalah ...
a.    50
b.    40
c.    30
d.    20
e.    10
PEMBAHASAN:
-    4x + y = 20
Jika x = 0, maka y = 20 ... (0, 20)
Jika y = 0, maka x = 5 .... (5, 0)
-    x + y = 20
jika x = 0, maka y = 20... (0, 20)
jika y = 0, maka x = 20 ... (20, 0)
-     x + y = 10
Jika x = 0, maka y = 10 ... (0, 10)
Jika y = 0, maka x = 10 ... (10, 0)
Yuk gambar lagi untuk mengetahui HP-nya:

-    Titik A (0, 20)
Maka nilai dari fungsi obyektif  z = 3x + 6y adalah: 3.0 + 6.20 = 120
-    Titik B adalah titik potong antara 4x + y = 20 dan x + y = 10, maka titik B adalah:

     10/3 + y = 10
     y = 10 – 10/3
     y = 30/3 – 10/3
     y = 20/3 ... titik B (10/3, 20/3)
Maka nilai dari fungsi obyektif  z = 3x + 6y adalah: 3.10/3 + 6.20/3 = 10 + 40 = 50
-    Titik C (20, 0)
Maka nilai dari fungsi obyektif  z = 3x + 6y adalah: 3.20 + 6.0 = 60
-    Titik D (10, 0)
Maka nilai dari fungsi obyektif  z = 3x + 6y adalah: 3.10 + 6.0 = 30
Sehingga, nilai minimalnya adalah 30
JAWABAN: C

5.  Disebuah kantin, Ani dan kawan-kawan memayar tidak lebih dari Rp35.000 untuk 4 mangkok bakso dan 6 gelas es yang dipesannya, sedang Adi dan kawan-kawan membayar tidak lebih dari Rp50.000,-  untuk 8 mangkok bakso dan 4 gelas es. Jika kita memesan 5 mangkok bakso dan 3 gelas es, maka maksimum yang harus kita bayar adalah ...
a.    Rp27.500,-
b.    Rp30.000,-
c.    Rp32.500,-
d.    Rp35.000,-
e.    Rp37.500,-
PEMBAHASAN:
Harga 1 mangkok bakso = x
Harga 1 gelas es = y
Kalimat matematika untuk soal di atas adalah:
4x + 6y ≤ 35000
8x + 4y ≤ 50000
x ≥ 0
y ≥ 0
Karena bakso dan gelas tidak mungkin 0, maka kita langsung saja mencari titik potong antara garis 4x + 6y = 35000 dan 8x + 4y = 50000:

    8x + 4(2500) = 50.000
    8x + 10.000 = 50.000
    8x = 40.000
     x = 5.000
Maka, harga maksimum untuk 1 mangkok bakso = Rp5.000,- dan harga maksimum untuk 1 gelas es adalah Rp2.500
Jika kita memesan 5 mangkok bakso dan 3 gelas es, maka maksimum yang harus kita bayar adalah: 5(5.000) + 3(2.500) = 25.000 + 7.500 = 32.500
JAWABAN: C

6. Tempat parkir seluas 600 m2 hanya mampu menampung bus dan mobil sebanyak 58 buah. Tiap mobil memerlukan tempat 6 m2 dan bus 24 m2. Biaya parkir tiap mobil Rp5.000,- dan bus Rp7.000,-. Jika tempat parkir penuh, hasil dari biaya parkir paling banyak adalah ...
a.    Rp197.500,-
b.    Rp220.000,-
c.    Rp290.000,-
d.    Rp325.000,-
e.    Rp500.000,-
PEMBAHASAN:
Mobil: x
Bus: y
Mampu menampung bus dan mobil sebanyak 58 buah = x + y ≤ 58
Tiap mobil memerlukan tempat 6 m2 dan bus 24 m2. Tempat parkir seluas 600 m2 = 6x + 24y ≤ 600
Fungsi obyektif = Biaya parkir tiap mobil Rp5.000,- dan bus Rp7.000,- = 5000x + 7000y
Mari kita kerjakan model matematika di atas:
-    x + y = 58
Jika x = 0,maka y = 58 ... (0, 58)
Jika y = 0, maka x = 58 ... (58, 0)
-    6x + 24y = 600
Jika x = 0, maka y = 25 ... (0, 25)
Jika y = 0, maka x = 100 ...(100, 0)
Yuk, kita gambar untuk mengetahui daerah hasilnya:

-    Titik A (0, 25)
Maka nilai obyektif untuk 5000x + 7000y = 5000(0) + 7000(25) = 187.500
-    Titik B adalah titik potong antara garis x + y = 58 dan 6x + 24y = 600, maka titik B adalah:

    14 + y = 58
    y = 44 ... titik B (14, 44)
Maka nilai obyektif untuk 5000x + 7000y = 5000(14) + 7000(44) = 220.000 + 105.000 = 325.000
-     Titik C (58, 0)
Maka nilai obyektif untuk 5000x + 7000y = 5000(58) + 7000(0) = 290.000
Jadi, hasil paling banyak adalah Rp325.000
JAWABAN: D

7.  Tanah seluas 10.000 m2 akan dibangun rumah tipe A dan tipe B. Untuk rumah tipe A diperlukan 100 m2 dan tipe B diperlukan 75 m2. Jumlah rumah yang dibangun paling banyak 125 unit. Keuntungan rumah tipe A adalah Rp6.000.000,-/ unit dan tipe B adalah Rp4.000.000,-/ unit. Keuntungan maksimum yang dapat diperoleh dari penjualan rumah tersebut adalah ...
a.    Rp550.000.000,-
b.    Rp600.000.000,-
c.    Rp700.000.000,-
d.    Rp800.000.000,-
e.    Rp900.000.000,-
PEMBAHASAN:
Rumah tipe A = x
Rumah tipe B = y
100x + 75y ≤ 10.000 atau 4x + 3y ≤ 400
x + y ≤ 125
fungsi obyektif = 6.000.000x + 4.000.000y
Kita gambar grafiknya yuk:
-    4x + 3y = 400
Jika x = 0, maka y = 400/3 ... (0, 400/3)
Jika y = 0, maka x = 100 ... (100, 0)
-    x + y = 125
jika x = 0, maka y = 125 ... (0, 125)
jika y = 0, maka x = 125 ... (125, 0)

-    titik A (0, 125)
Maka nilai fungsi obyektif 6.000.000x + 4.000.000y = 6.000.000(0) + 4.000.000(125) = 500.000.000
-    titik B adalah titik potong 4x + 3y = 400 dan x + y = 125, maka titik B adalah:

    x + 100 = 125
    x = 25 ... titik B (25, 100)
Maka nilai fungsi obyektif 6.000.000x + 4.000.000y = 6.000.000(25) + 4.000.000(100) = 150.000.000 + 400.000.000 = 550.000.000
-     titik C (100, 0)
Maka nilai fungsi obyektif 6.000.000x + 4.000.000y = 6.000.000(100) + 4.000.000(0) = 600.000.000
Jadi, keuntungan maksimumnya 600.000.000
JAWABAN: B

8. Seorang peternak ikan hias memiliki 20 kolam untuk memelihara ikan koi dan ikan koki. Setiap kolam dapat menampung ikan koki saja sebanyak 24 ekor, atau ikan koi saja sebanyak 36 ekor. Jumlah ikan yang direncanakan akan dipelihara tidak lebih dari 600 ekor. Jika banyak kolam berisi ikan koki adalah x, dan banyak kolam berisi ikan koi y, maka model matematikanya adalah ...
a.    x + y ≥ 20; 3x + 2y ≤ 50; x ≥ 0; y ≥ 0
b.    x + y ≥ 20; 2x + 3y ≤ 50; x ≥ 0; y ≥ 0
c.    x + y ≤ 20; 2x + 3y ≤ 50; x ≥ 0; y ≥ 0
d.    x + y ≤ 20; 2x + 3y ≥ 50; x ≥ 0; y ≥ 0
e.    x + y ≤ 20; 3x + 2y ≥ 50; x ≥ 0; y ≥ 0
PEMBAHASAN:
Ikan koki = x
Ikan koi = y
-    20 kolam untuk memelihara ikan koi dan ikan koki = x + y ≤ 20
-    Setiap kolam dapat menampung ikan koki saja sebanyak 24 ekor, atau ikan koi saja sebanyak 36 ekor. Jumlah ikan yang direncanakan akan dipelihara tidak lebih dari 600 ekor = 24x + 36y ≤ 600 atau 2x + 3y ≤ 50
-    x ≥ 0
-    y ≥ 0
JAWABAN: C

9.Pedagang buah memiliki modal Rp. 1.000.000,00 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kg apel Rp 4000,00 dan pisang Rp 1.600,00. Tempatnya hanya bisa menampung 400 kg buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum.

Pembahasan

Diketahui:

Dengan syarat:

• Kapasitas tempat: x + y ≤ 400
• Modal: 4.000x + 1.600y ≤ 1.000.000
• x ≥ 0
• y ≥ 0

Diagramnya:

Titik ekstrim:

• A(0, 400) bukan optimum karena tidak ada apel
• C(250, 0) bukan optimum karena tidak ada pisang
• dengan metode eliminasi 2 persamaan diatas diperoleh:

Sehingga jumlah masimum:

• Apel: 150 kg
• Pisang: 250 kg    

10. Seorang pedagang minuman menjual dua jenis minuman ringan pada suatu tempat yang dapat menampung 500 botol minuman. Harga beli minuman jenis A dan jenis B masing-masing Rp. 2000 dan Rp 4000 per botol. Jika ia memiliki modal Rp. 1.600.000 serta akan memperoleh laba perbuah Rp. 800 untuk minuman jenis A dan Rp. 600 untuk minuman jenis B, maka berapakah banyaknya minuman minuman jenis A dan B agar diperoleh laba maksimum ?
pembahasan;
Misalkan
x = banyaknya minuman jenis A
y = banyaknya minuman jenis B
maka dapat disusun kendala modal dan kapasitas kios sebagai berikut:
x + y ≤ 500
2000x + 4000y ≤ 1.600.000
x ≥ 0
y ≥ 0
Jika disederhanakan menjadi :
x + y ≤ 500
x + 2y ≤ 800
x ≥ 0
y ≥ 0
Fungsi laba : f(x, y) = 800x + 600y
Selanjutnya akan dilukis grafik daerah penyelesaian sistem pertidaksamaan di atas

Titik A koordinatnya adalah A(0, 400)
Titik C koordinatnya adalah C(500, 0)
Sedangkan titik B merupakan perpotongan garis g dan h, diperoleh :

karena x + y = 500 maka x + 300 = 500, sehingga x = 200
Jadi koordinat titik B adalah B(200, 300)
Selanjutnya titik-titik tersebut disubstitusikan ke dalam fungsi optimum yakni f(x,y) = 800x + 600y, sehingga diperoleh :
A(0, 400)     → f(A) = 800(0) + 600(400) = 240.000
B(200, 300) → f(B) = 800(200) + 600(300) = 360.000
C(500, 0)     → f(C) = 800(500) + 600(0) = 400.000
Jadi keuntungan maksimum yakni sebesar Rp. 400.000 diperoleh jika dijual minuman jenis A saja sebanyak 500 botol

daftar pustaka

 https://www.ajarhitung.com/2017/02/contoh-soal-dan-pembahasan-tentang_7.html

PENYELESAIAN PERTIDAKSAMAAN PROGRAM LINEAR

SAYA ALIYA RAHMAH XI IPS 2 AKAN MEMBERIKAN PENYELESAIAN PERTIDAKSAMAAN PROGRAM LINEAR DENGAN MENGGUNAKAN DAERAH BERSIH ATAU DAERAH KOTOR.

 

DARI PERTIDAKSAMAAN 3x + 2y ≤ 12, 5x + 3y < 19, x ≥ 0 y ≥ 0

pembahasan;

1. 3x + 2y ≤ 12                                                             2. 5x + 3y < 19

jika digambar grafiknya maka akan seperti iniDaerah Bersih 

Daerah Kotor

 uji coba titik pada (0,0)

1. 3x + 2y      ≤  12      

    3(0) + 2(0) ≤  12

            0         ≤  12 (benar)      

 2. 5x + 3y      < 19

    5(0) + 3(0)  < 19

            0          < 19 (benar)

JADI HIMPUNAN PENYELESAIAN DARI PERTIDAKSAMAAN 3x + 2y ≤ 12, 5x + 3y < 19, x ≥ 0  y ≥ 0 ADALAH DAERAH YANG DIARSIR PADA  DAERAH BERSIH.

Note:  1.  jika uji coba titik benar maka arsiran ke arah bawah atau kanan jika uji coba titik salah maka arsiran ke atas atau kanan.

             2.  Jika x ≥ 0 dan y ≥ 0 berarti arsiran keatas atau kekanan

             3.  JIka tanda > atau < maka garis putus-putus

daftar pustaka

https://youtu.be/Z.Z38OSx0whw

program linear

assalamualaikum wr.wb 
saya aliya rahmah XI IPS 2 ingin memberikan materi-materi program linear.

Program Linear 

A. PENDAHULUAN 
 Program linear adalah suatu program untuk menyelesaikan permasalahan yang batasbatasannya berbentuk sistem pertidaksamaan linear dua variabel (SPTLDV).   
Program linear mempelajari empat hal utama: 
1) Menggambar daerah penyelesaian (DP) dari PTLDV atau SPTLDV. 
2) Menentukan PTLDV atau SPTLDV dari daerah penyelesaian. 
3) Menentukan nilai optimum (nilai maksimum dan minimum) pada daerah penyelesaian. 
4) Menyelesaikan masalah mengenai optimasi yang berkaitan dengan program linear. 

B. MENENTUKAN DAERAH PENYELESAIAN 
 Daerah penyelesaian merupakan himpunan penyelesaian (nilai benar) dari PTLDV atau SPTLDV.  Daerah penyelesaian dapat dibuktikan melalui pendekatan grafik pada bidang kartesius.  
Langkah menentukan DP: 
1) Tentukan dua buah titik sembarang dari pertidaksamaan. 
2) Tarik garis sehingga kedua titik terhubung dan membagi bidang kartesius menjadi dua bagian. 
3) Periksa/uji nilai titik di salah satu bagian yang telah terbagi tadi, dengan memasukkan nilai x dan y titik ke pertidaksamaan. 
4) Jika daerah yang terdapat titik yang diuji nilainya bernilai benar, maka itulah daerah penyelesaian. Jika tidak, maka daerah penyelesaiannya berada di bidang lawannya. 
5) Jika pertidaksamaan mempunyai sama dengan, maka titik-titik pada garis juga merupakan daerah penyelesaian. Jika pertidaksamaan tidak mempunyai sama dengan, maka titik-titik pada garis bukan daerah penyelesaian.
 Contoh: Tentukan daerah penyelesaian dari SPTLDV berikut ini:
 x ≥ 0 …(1) 
y ≥ 0 …(2) 
2x + 5y ≥ 10 …(3) 
4x + y > 8 … (4) 

C. PERSAMAAN GARIS  
Persamaan garis dapat dibentuk dari suatu garis pada bidang kartesius. 

 D. MENENTUKAN SPTLDV DARI DAERAH PENYELESAIAN 
 Cara menentukan PTLDV dan SPTLDV dari grafik daerah penyelesaian: 
1) Jumlah garis pembatas daerah penyelesaian adalah jumlah SPTLDV. 
2) Tentukan semua persamaan garis dengan rumus-rumus pada pembahasan sebelumnya. 
3) Uji nilai titik di salah satu bagian yang dibagi garis untuk menentukan tanda pertidaksamaan yang tepat. 
Contoh: Tentukan pertidaksamaan-pertidaksamaan yang memenuhi daerah penyelesaian berikut ini!

Garis 1
 -4x + 8y  = -4. 8    
 x – 2y      = 8
 Uji titik koordinat untuk (0, 0) (daerah benar)
 (0) – 2(0) = 8 0 = 8, 
tandanya adalah ≤ dan titik berada di daerah benar,
 maka x – 2y ≤ 8 

Garis 2 (tegak lurus dengan garis 1) Tentukan titik potongnya terlebih dahulu dengan garis 1 (diketahui x = 12)      
 x - 2y   = 8   
 12 – 2y = 8           
   y         = 2 
berpotongan pada (12, 2), 
maka  2x + y = 2. 12 + 1. 2   
   2x + y = 26
 Uji titik koordinat untuk (0, 0) (daerah benar) 2(0) + (0) = 26
 0 = 26, tandanya adalah ≤ dan titik berada di daerah benar, 
maka 2x + y ≤ 26

Garis 3 (berpotongan dengan garis 2) 
Tentukan titik potongnya dengan garis 2 (diketahui y = 12)       
2x + y  = 26    
 2x + 12  = 26              
 x  = 7 berpotongan pada (7, 12), dan ada titik pada 0, 0, 
maka 12x + 7y = 0 
Uji titik koordinat untuk (1, 0) (daerah benar) 
12(1) + 7(0) = 0 12 = 0, tandanya adalah ≥ dan titik berada di daerah benar,
 maka 12x + 7y ≥ 0

Garis 4     
3x + 4y = 4. 3    
 3x + 4y = 12 Uji titik koordinat untuk (0, 0) (daerah salah)
 3(0) + 4(0) = 12 0 = 12, tandanya adalah ≤ dan titik berada di daerah salah,
 maka 3x + 4y ≥ 12 E

contoh soal

1.    Nilai maksimum f(x, y) = 5x + 4y yang memenuhi pertidaksamaan x + y ≤ 8, x + 2y ≤ 12, x ≥ 0, dan y ≥ 0 adalah ...
a.    24
b.    32
c.    36
d.    40
e.    60
PEMBAHASAN:
-    x + y ≤ 8
ketika x = 0, maka y = 8 .... (0, 8)
ketika y = 0, maka x = 8 .... (8, 0)
-    x + 2y ≤ 12
ketika x = 0, maka y = 6 .... (0, 6)
ketika y = 0, maka x = 12 .... (12, 0)
Sehingga, grafik dari pertidak samaan di atas adalah:

Kita cari dulu titik B, yaitu titik potong dua buah garis, yaitu:

subtitusikan y = 4 dalam x + y = 8
x + 4 = 8
x = 4 .... (4, 4)
Jadi, nilai fungsi obyektifnya adalah:
f(x, y) = 5x + 4y
-    titik A (0, 6)
      5x + 4y = 5.0 + 4.6 = 24
-    titik B (4, 4)
      5x + 4y = 5.4 + 4.4 = 20 + 16 = 36
-    titik C (8, 0)
      5x + 4y = 5.8 + 4.0 = 40
Jadi, nilai maksimumnya adalah 40.
JAWABAN: D

2.    Nilai minimum fungsi obyektif  f(x, y) = 3x + 2y dari daerah yang diarsir pada gambar adalah  ...

a.    4
b.    6
c.    7
d.    8
e.    9
PEMBAHASAN:
Perhatikan gambar berikut:

Ingat ya, rumus persamaan garis yang melalui titik (0, a) dan (b, 0) adalah: ax + by = a.b, maka:
-    Persamaan garis p = 4x + 2y = 4.2 = 4x + 2y = 8 = 2x + y = 4
-    Persamaan garis q = 3x + 3y = 3.3 = 3x + 3y = 9 = x + y = 3
Selanjutnya, kita cari titik potong garis p dan q, yaitu di titik B:

subtitusikan x = 1 dalam x + y =3
1 + y = 3
y = 2 .... B(1, 2)
kita cari nilai dari fungsi obyektif  f(x, y) = 3x + 2y:
-    Titik A (0, 4)
     3x + 2y = 3.0 + 2.4 = 8
-    Titik B (1, 2)
      3x + 2y = 3.1 + 2.2 = 7
-    Titik C (3, 0)
      3x + 2y = 3.3 + 2.0 = 9
Jadi, nilai minimumnya adalah 7
JAWABAN: C

3.    Daerah yang merupakan himpunan penyelesaian dari pertidaksamaan 2x + 3y ≤ 12, 4x + y ≥ 10, x ≥ 0, y ≥ 0 adalah ...

a.    I
b.    II
c.    III
d.    IV
e.    I dan III
PEMBAHASAN:
-    Daerah hasil 2x + 3y ≤ 12 adalah area II dan III
-    Daerah hasil  4x + y ≥ 10 adalah area III dan IV
Maka, yang mencakup keduanya adalah area nomor III
JAWABAN: C

  4.    Daerah mana yang diarsir di bawah ini adalah daerah penyelesaian suatu sistem pertidaksamaan. Nilai maksimum fungsi objektif (3x + 5y) pada daerah penyelesaian tersebut ...

a.    30
b.    26
c.    24
d.    21
e.    18
PEMBAHASAN:
Perhatikan gambar:

-    Persamaan garis p = 6x + 4y = 24 atau 3x + 2y = 12
-    Persamaan garis q = 4x + 6y = 24 atau 2x + 3y = 12
Titik potong garis p dan q adalah:

subtitusikan y = 12/5 dalam 2x + 3y = 12:
2x + 3.12/5 = 12
2x = 12 – 36/5
2x = 60/5 – 36/5
2x = 24/5
x = 24/10 = 12/5 .... titik B (12/5, 12/5)
Nilai dari fungsi obyektif  3x + 5y adalah:
-    Titik A (0, 6)
      3x + 5y = 3.0 + 5. 6 = 30
-    Titik B (12/5, 12/5)
      3x + 5y = 3.12/5 + 5.12/5 = 36/5 + 60/5 = 96/5 = 19,2
-    Titik C (6, 0)
      3x + 5y = 3.6 + 5.0 = 18
Jadi, nilai minimumnya adalah 18
JAWABAN: E

5. Nilai maksimum dari z = -3x + 2y yang memenuhi syarat 3x + y ≤ 9, 5x + 4y ≥ 20, x ≥ 0 adalah ...
a.    10
b.    14
c.    18
d.    20
e.    24
PEMBAHASAN:
-    3x + y ≤ 9
Jika x = 0, maka y = 9 .... (0, 9)
Jika y = 0, maka x = 3 .... (3, 0)
-    5x + 4y ≥ 20
Jika x = 0, maka y =5 ..... (0, 5)
Jika y = 0, maka x = 4 .... (4, 0)
Kita cari daerah hasilya dengan menggambarnya:

Kita cari dulu titik potong kedua garis di titik B:

subtitusikan x = 16/7 dalam 3x + y = 9
3.16/7 + y = 9
48/7 + y = 9
y = 9 – 48/7
y = 63/7 – 48/7
y = 15/7 ... titik B (16/7, 15/7)
Kita cari nilai dari fungsi obyektif  z = -3x + 2y:
-    Pada titik A (0, 9)
      -3x + 2y = -3.0 + 2.9 = 18
-    Pada titik B (16/7, 15/7)
     -3x + 2y = -3.16/7 + 2.15/7 = -48/7 + 30/7 = -18/7
-    Pada titik C (0, 5)
     -3x + 2y = -3.0 + 2.2 = 4
Jadi, nilai maksimumnya adalah 18.
JAWABAN: C

DAFTAR PUSTAKA

https://materi78.wordpress.com